Alg.00.常用数据结构 Quick View

分类于
字数统计: 2,526

1.线性结构(Linear structures)

Alg.11.数据结构-线性结构

「逻辑结构」揭示了数据元素之间的逻辑关系。在数组和链表中，数据按照顺序依次排列，体现了数据之间的线性关系；而在树中，数据从顶部向下按层次排列，表现出祖先与后代之间的派生关系；图则由节点和边构成，反映了复杂的网络关系。

逻辑结构通常分为「线性」和「非线性」两类。线性结构比较直观，指数据在逻辑关系上呈线性排列；非线性结构则相反，呈非线性排列，例如网状或树状结构。

  • 线性数据结构：数组、链表、栈、队列；
  • 非线性数据结构：树、图、堆、哈希表；

2.树(Tree)

Alg.12.数据结构-树

树相关概念

  • 树的阶: 一个节点拥有的子节点最大值, 二叉树的阶是 2
  • 树的度: 同阶的概念, 为什么 B-tree 在不同著作中度的定义有一定差别？ - 知乎
  • 叶子节点: 没有子节点的节点,称为叶子节点
  • 节点的高度: 到最深树叶的路径长度
  • 节点的深度: 节点到根节点的距离(根节点深度为 0)
  • 树的高度: 根节点的高度

常见树结构

Tree

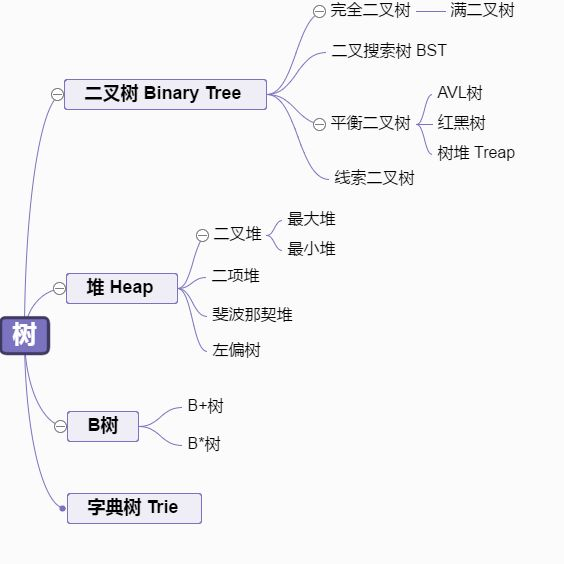
二叉树

二叉树: 每个节点的叶子不超过2

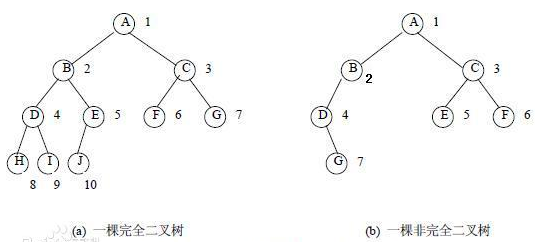
完全二叉树

完全二叉树: 若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树

完全二叉树

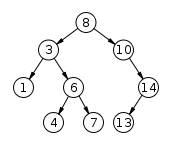
二叉搜索树 BST

二叉搜索树（BST / BinarySearchTree）特性:

  • 对于树中某个节点X, 左子树中所有值都小于X, 右子树所有值都大于X; 不足: 但是当原序列有序时二叉搜索树为右斜树，同时二叉树退化成单链表，搜索效率降低为 O(n)。时间复杂度:
    • 索引: O(log(n))
    • 搜索: O(log(n))
    • 插入: O(log(n))
    • 删除: O(log(n))

二叉搜索树

平衡二叉树 AVL

平衡二叉树（AVL）特性:

  • 极端情况下的 BST 可能退化为链表，AVL 即一种为改进的二叉查找树。一般的二叉查找树的查询复杂度取决于目标结点到树根的距离（即深度），因此当结点的深度普遍较大时，查询的均摊复杂度会上升[1]。为了实现更高效的查询，产生了平衡树。
  • 平衡二叉树的特点：任何节点的左右子树高度差不超过1;
  • 在构造平衡二叉树时，需要采用不同的调整方式，使得二叉树在插入数据后保持平衡。主要的四种调整方式有LL（左旋）、RR（右旋）、LR（先左旋再右旋）、RL（先右旋再左旋）

红黑树 RB

红黑树（Red Black Tree） 特性:

  • 红黑树也是一种 AVL（带平衡条件的搜索树）。
  • 红黑树在每个节点增加一个存储位表示节点的颜色，可以是红或黑（非红即黑）。

字典树 Tire

字典树（Trie Tree）特性:

  • 根节点不包含字符，除根节点外的每一个子节点都包含一个字符
  • 从根节点到某一节点，路径上经过的字符连接起来，就是该节点对应的字符串
  • 每个字符串的公共前缀作为一个字符节点保存

例：如果我们有 and,as,at,cn,com 这些关键词，那么构建的 trie 树如下

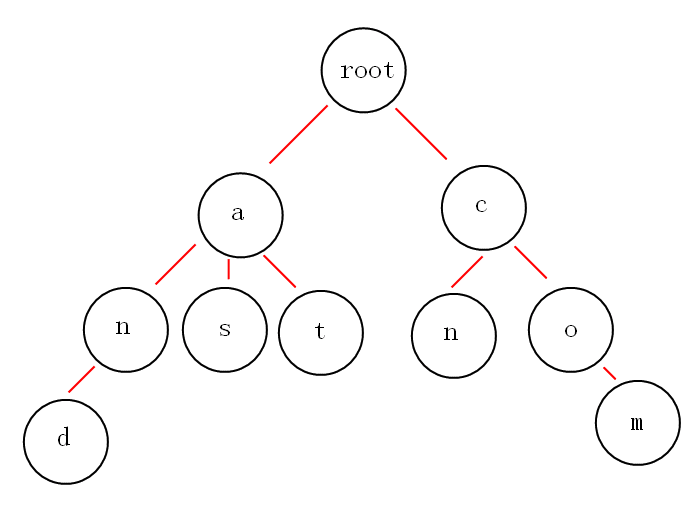
../_images/TrieTreeExample.png

Trie 树就是利用字符串之间的公共前缀，将重复的前缀合并在一起。

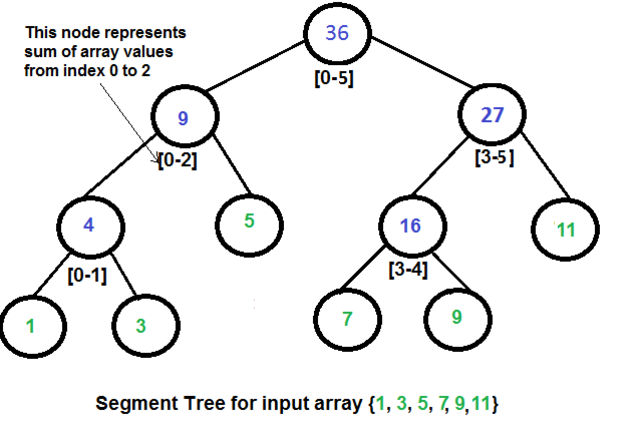
线段树 Segment

线段树（Segment Tree or Interval tree）特性：

  • 线段树是用于存放间隔或者线段的树形数据结构，它允许快速的查找某一个节点在若干条线段中出现的次数.
  • 时间复杂度:
    • 区间查询: O(log(n))
    • 更新: O(log(n))

../_images/Segment-Tree.png

B 树 ~ B+树

B-树: “Balance Tree”, 阶为 M 的B树满足如下特性:

  • 树的 根节点 拥有的子节点数量子在 2- M 之间；
  • 除根外，每个 非叶子节点 拥有的子节点数量在 M/2 - M 之间；
  • 一个 非叶子节点 如果包含 k 个关键字，那么它有 k+1 个子节点；
  • 所有叶子节点都在相同的深度，且叶子节点不包含关键字信息；

B+树:

  • 要存储的数据只在叶子节点中, 非叶子节点不存储数据, 只有关键字;
  • 相邻的叶子节点之间都有一个链指针，不需要遍历整棵树就可以得到所存储的全部数据

@link:: [[../32.Database/MySQL-02b-BTree索引原理]]

3.散列表(Hash Table)

Alg.13.数据结构-散列表

  • 散列（Hash，也译作哈希）能够将任意长度的数据映射到固定长度的数据。散列函数返回的即是哈希值，如果两个不同的键得到相同的哈希值，即将这种现象称为碰撞。

  • 散列表（Hash table，也译作哈希表），它通过哈希函数把 Key 的值映射到表中一个位置，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。

https://zh.wikipedia.org/zh-hans/%E5%93%88%E5%B8%8C%E8%A1%A8

4.图(Graph)

Alg.14.数据结构-图

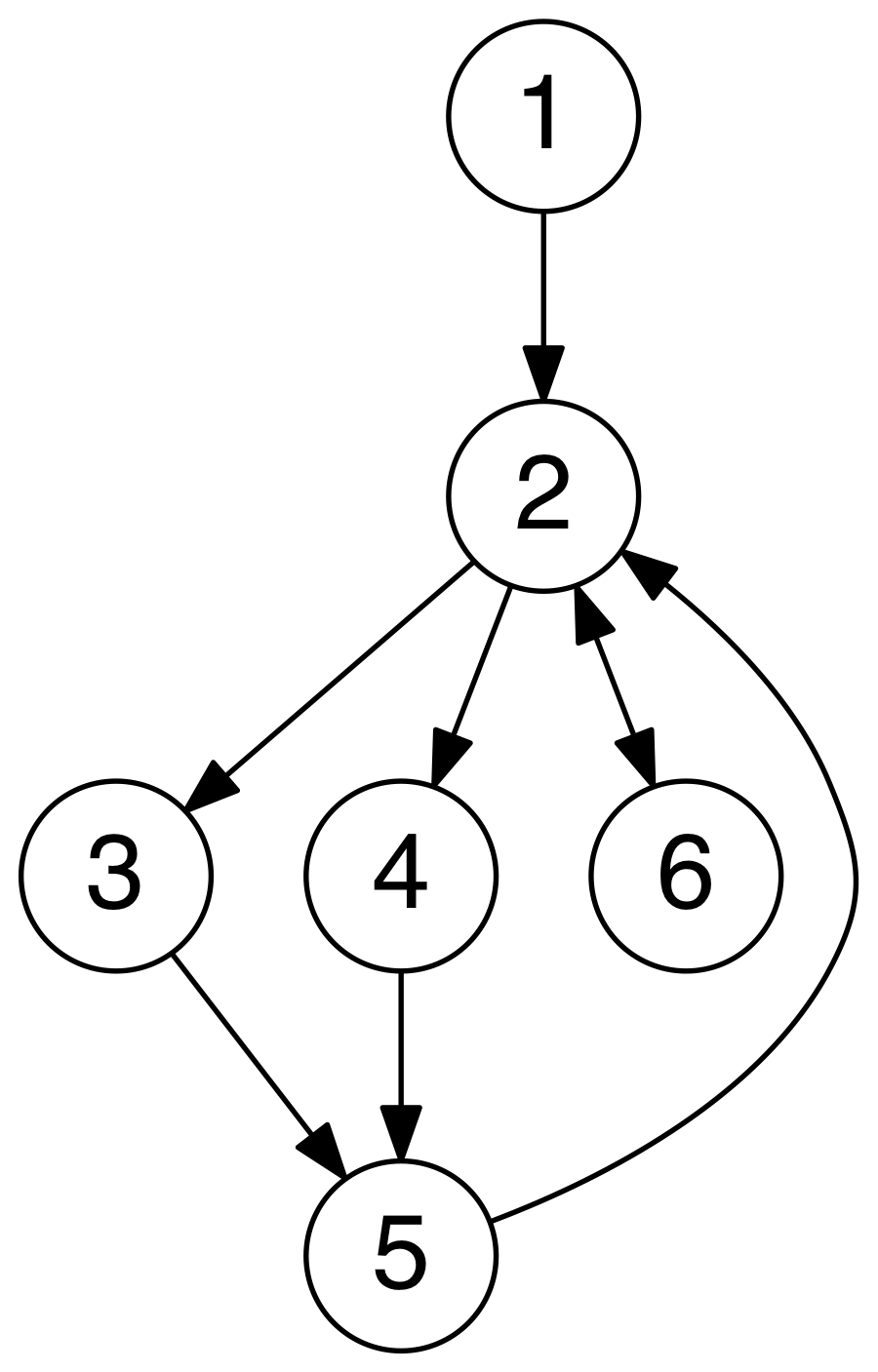
图形结构是一种比树形结构更复杂的非线性结构。在树形结构中，结点间具有分支层次关系，每一层上的结点只能和上一层中的至多一个结点相关，但可能和下一层的多个结点相关。而在图形结构中，任意两个结点之间都可能相关，即结点之间的邻接关系可以是任意的。

  • 无向图（Undirected Graph）: 无向图具有对称的邻接矩阵，因此如果存在某条从节点 u 到节点 v 的边，反之从 v 到 u 的边也存在。
  • 有向图（Directed Graph）: 有向图的邻接矩阵是非对称的，即如果存在从 u 到 v 的边并不意味着一定存在从 v 到 u 的边。
    ../_images/Alg.00.数据结构-Quick View-Graph.png

https://zh.wikipedia.org/zh-hans/%E5%9B%BE_(%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84)

5.堆(Heap)

堆（Heap）是一种特别的完全二叉树。若是满足以下特性，即可称为堆积：“给定堆积中任意节点 P 和 C，若 P 是 C 的父节点，那么 P 的值总是小于等于（或大于等于）C 的值”。

  • 若父节点的值恒小于等于子节点的值，此堆积称为最小堆积（min heap）；
  • 反之，若父节点的值恒大于等于子节点的值，此堆积称为最大堆积（max heap）；

二叉堆

JDK 中的 PriorityQueue 通过二叉堆实现 @link:: Alg.15.数据结构-堆

二叉堆

二叉堆（Binary Heap）特性:

  • 堆是一种特别的完全二叉树（除了最后一层，其他层的节点个数都是满的，最后一层的节点都靠左排列）；
  • 如果父节点的键值总是小于或等于子节点（根节点的值是最小的）, 那么称为小顶堆（min heap），反正择称为大顶堆（max heap）
  • 二叉堆是完全二叉树的特点，可以使用数组存储：
    • 根节点在位置0
    • 任意一个父节点设在位置 i，那么左子节点在位置 2i+1，右子节点在位置 2i+2

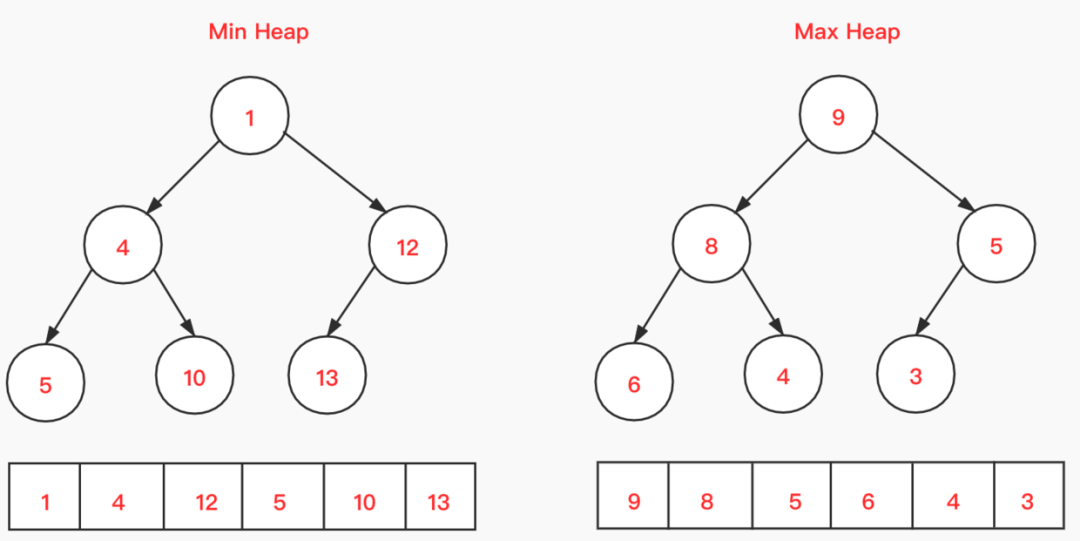
../_images/BinaryHeapArray.png

二叉堆一般用数组来表示。如果根节点在数组中的位置是1，第_n_个位置的子节点分别在2_n_和 2_n_+1。因此，第1个位置的子节点在2和3，第2个位置的子节点在4和5。以此类推。这种基于1的数组存储方式便于寻找父节点和子节点。

如果存储数组的下标基于0，那么下标为 i 的节点的子节点是2i + 1与 2i + 2；其父节点的下标是 $ floor((i − 1) ∕ 2) $。

floor(_x_)的功能是“向下取整”，或者说“向下舍入”，即取不大于_x_的最大整数（与“四舍五入”不同，向下取整是直接取按照数轴上最接近要求值的左边值，即不大于要求值的最大的那个值）。比如 floor(1.1)、floor(1.9)都返回1。

斐波那契堆

➤ 常见的堆结构，除了上面提到的大小堆，还有斐波那契堆 (Fibonacci heap)：

裴波那契堆（Fibonacci Heap）是由 Michael L. Fredman 和 Robert E. Tarjan 在 1984 年发明的一种数据结构，它是一种可合并堆 （mergeable heap）。

裴波那契堆的特点是可以在 O(1)时间内插入单个元素，O(logn)时间内删除最小元素，O(1)时间内合并两个堆。同时，裴波那契堆的平均时间复杂度比二叉堆（Binary Heap）低，因此在某些应用中具有优势。

裴波那契堆的核心思想是利用裴波那契数列的特性来实现堆的操作。裴波那契数列是一个数列，其中每个数字都是前两个数字之和，数列的前几项为：0，1，1，2，3，5，8，13，21，34，…… 等。

裴波那契堆的节点中除了存储元素的值之外，还存储了节点的度数和父节点指针、左右子节点指针以及兄弟节点指针等信息。在堆的合并操作中，裴波那契堆采用了一种“合并根链”的方式，将两个堆中最小的根节点合并，并通过指针将两个堆的根链连接起来。

裴波那契堆的实现比较复杂，但是在某些应用场景下能够提供更好的效率。比如在 Prim 算法中，使用裴波那契堆可以将时间复杂度优化到 O(E+VlogV)。